Evaluación Alumno
| 1|38% | 2|68% | 3|61% | 4|85% | 5|69% | 6|93% | 7|95% | 8|63% | 9|68% | 10|90% | 11|?? | Promedio|73% |
|---|
Secciones y Reactivos
Instrucciones: Selecciona los reactivos que desees, la respuesta correcta aqui es la a) para los alumnos aparecerá de forma aleatoria.
1)
✓ Muy bien esa transposición no se hizo adecuadamente.
Recuerda que debes dividir la misma cantidad en ambos lados de la ecuación.

a) 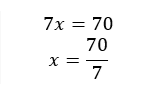
b) 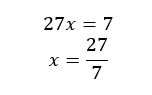
c) 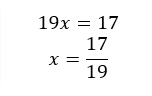
d) 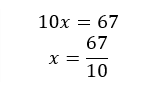
2)
✓ Bien, el ocho se restó en ambos lados.
Recuerda que debes sumar o restar la misma cantidad en ambos lados para que sume 0 en el lado que quieres eliminarla.

a) 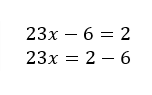
b) 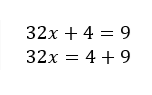
c) 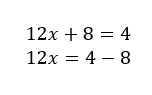
d) 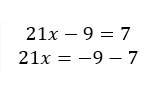
3)
✓ Correcto, ya que 20×13=260
Recuerda que al transponer un elemento que divide, del otro lado de la ecuación multiplica.

a) 
b) 
c) 
d) 
4)
✓ Correcto, porque x=10/10
Recuerda que al transponer el coeficiente b hay un cambio de signo y el coeficiente a que multiplica al transponerlo divide.

a) 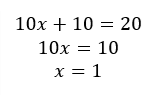
b) 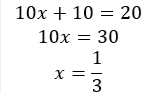
c) 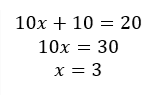
d) 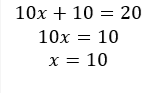
5)
✓ Correcto, porque queda 17x-13x=8+14
Recuerda que al transponer buscamos que los términos de x queden en un lado de la ecuación y los demás términos en el otro lado, sumando o restando de acuerdo con los cambios de signo.

a) 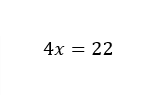
b) 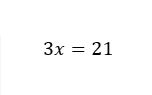
c) 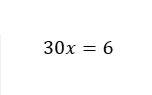
d) 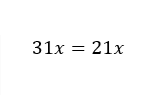
Instrucciones: Selecciona los reactivos que desees, aqui aparece la respuesta correcta, para los alumnos no aparece.
| N | Frase | V | F | |
|---|---|---|---|---|
| 1 | Asignar una literal para plantear una ecuación lineal significa identificar una cantidad desconocida. | ✓ Correcto, asignar una literal es un paso posterior a identificar la cantidad desconocida. Recuerda que asignas la literal una vez que sabes cuál es la cantidad desconocida. | ||
| 2 | En una ecuación lineal del tipo ax+b=c, los coeficientes a, b y c pueden tomar cualquier valor. | ✓ Así es, el coeficiente a no puede tomar el valor 0. Recuerda que si el coeficiente a vale 0, entonces no es una ecuación lineal, por lo que no puede tomar cualquier valor. | ||
| 3 | “Expresar una relación matemática” implica traducir la relación entre cantidades conocidas en términos matemáticos. | ✓ Correcto. Recuerda que una relación matemática implica describir numéricamente cómo interactúan las cantidades en una situación. | ||
| 4 | El siguiente desarrollo es correcto: 16x+120=280 16x=280-120 16x=160 x=160/16 x=10 |
✓ Así es, el desarrollo tiene un procedimiento sin errores. Recuerda que la transposición de términos que suman o restan y que multiplican o dividen sirven para ir aislando la variable x e igualarla a un número. | ||
| 5 | En la ecuación x/24=8, se puede transponer el 24 para que quede 8/24 | ✓ Correcto, la transposición de una cantidad que divide resulta en un producto. Recuerda que debes multiplicar en ambos lados de la ecuación para eliminar una cantidad que divide. |
Relación
Instrucciones: La forma general de plantear un modelo matemático de ecuación lineal es la siguiente:
✓ Correcto, el orden de los pasos ayuda a encontrar el valor desconocido. Recuerda que partimos de identificar la cantidad que se desconoce, para luego plantear la forma de relacionar los datos y calcular el valor desconocido.
| N | Concepto 1 | Concepto 2 | |
|---|---|---|---|
| 1 | Identificar la incógnita | ¿Qué relación hay entre las cantidades involucradas? | |
| 2 | Asignar una variable | ¿Cuál cantidad desconozco? | |
| 3 | Expresar la relación matemática | ¿Cómo escribo la relación entre las cantidades involucradas? | |
| 4 | Escribir la ecuación lineal | ¿Cuánto vale la cantidad desconocida? | |
| 5 | Resolver la ecuación | ¿Cómo represento esa cantidad? |
Relación
Instrucciones: Acomoda la suma correcta de términos semejantes de x en cada caso:
✓ Correcto, transponemos el valor menor de x y sumamos o restamos. Recuerda que al transponer sumamos en ambos lados cada término, en general buscamos transponer el valor menor de x para obtener un valor positivo.
| N | Concepto 1 | Concepto 2 | |
|---|---|---|---|
| 1 | 4x+4=4+x | 5x | |
| 2 | 4x-4=2x-4 | 3x | |
| 3 | 4x-4=4-x | x | |
| 4 | 2x-4=4-2x | 2x | |
| 5 | 2x+4=x+4 | 4x |
Relación
Instrucciones: Una suscripción mensual al cine cuesta 100 pesos, más 40 pesos por cada película que se ve. Si una persona pagó 260 pesos en total, ¿cuántas películas vio ese mes?
✓ Correcto, esas descripciones corresponden a los pasos. Recuerda que partimos de definir la cantidad desconocida, establecer una variable, definir relaciones y expresarlas matemáticamente para calcular un valor.
| N | Concepto 1 | Concepto 2 | |
|---|---|---|---|
| 1 | Paso 1 | 100 + 40x = 260 | |
| 2 | Paso 2 | Sea x el número de películas vistas. | |
| 3 | Paso 3 | Cantidad de películas vistas. | |
| 4 | Paso 4 | x = 160 / 40 = 4 | |
| 5 | Paso 5 | Pago total = cuota fija (100) + 40 pesos por cada película |
Relación
Instrucciones: Relaciona cada ecuación con los coeficientes correctos:
✓ Así es, esa combinación de coeficientes corresponde a cada caso. Recuerda identificar cada coeficiente en la expresión general ax+b=c, no importa de qué lado de la ecuación estén, sino la función que desempeñan.
| N | Concepto 1 | Concepto 2 | |
|---|---|---|---|
| 1 | 7x+6=9 | a,b,c | |
| 2 | 5=5+3x | c,a,b | |
| 3 | 9-4x=4 | a,c | |
| 4 | 6=2x-5 | c,b,a | |
| 5 | 8x=7 | b,a,c |
Relación
Instrucciones: Acomoda las ecuaciones que son equivalentes:
✓ Bien, esas ecuaciones son equivalentes al sumar términos semejantes. Recuerda que al sumar términos semejantes buscamos que la variable x siempre sea positiva el transponer términos.
| N | Concepto 1 | Concepto 2 | |
|---|---|---|---|
| 1 | 3x+6=12x-8 | 9=4x | |
| 2 | 8+12x=12-3x | 9x=4 | |
| 3 | 12x+3=6x+8 | 14=9x | |
| 4 | 8x+3=12x-6 | 15=2x | |
| 5 | 6x+3=8x-12 | 6x=5 |
Instrucciones: Selecciona los bloques de canevá que desees sean completados por los alumnos. Usted puede ver las respuestas correctas, los alumnos deberán seleccionarlas.
Una ecuación lineal es una expresión que involucra una incógnita elevada a la potencia y está igualada a una o a otra expresión.
En un evento se vendieron boletos a 25 pesos cada uno. Además, se cobró una tarifa única de 100
pesos por el uso del salón. Si se recaudaron 475 pesos, ¿cuántos boletos se vendieron?
Paso 1. Identifica la .
Cantidad de boletos vendidos.
Paso 2. Asigna una variable.
Sea x el número de vendidos.
Paso 3. Expresa la relación matemática.
CT = + 25x
Paso 4. Escribe la ecuación lineal.
100 + 25x =
Paso 5. Resuelve la ecuación.
25x = 475 - 100
25x = 375
x = 375 / = 15
→ Se vendieron 15 boletos.
Un fotógrafo cobra 200 pesos por la sesión, más 30 pesos por cada foto impresa. Si el cliente pagó
380 pesos, ¿cuántas fotos se imprimieron?
Paso 1. Identifica la incógnita.
Cantidad de impresas.
Paso 2. Asigna una variable.
Sea x el número de fotos.
Paso 3. Expresa la relación matemática.
CT = 200 + x
Paso 4. Escribe la ecuación lineal.
+ 30x = 380
Paso 5. Resuelve la ecuación.
30x = 380 - 200
30x =
x = 180 / 30 =
→ Se imprimieron 6 fotos
Un técnico cobra pesos por la visita y 50 pesos por cada hora de trabajo. Si el total fue de
230 pesos, ¿cuántas horas trabajó?
Paso 1. Identifica la incógnita.
Cantidad de horas trabajadas.
Paso 2. Asigna una variable.
Sea x el número de horas.
Paso 3. Expresa la relación matemática.
CT = 80 + 50x
Paso 4. Escribe la ecuación lineal.
80 + = 230
Paso 5. Resuelve la ecuación.
50x = 230 - 80
50x =
x = 150 / = 3
→ Trabajó 3 horas.
Una suscripción mensual al cine cuesta pesos, más pesos por cada película que se ve.
Si una persona pagó 260 pesos en total, ¿cuántas vio ese mes?
Paso 1. Identifica la incógnita.
Cantidad de películas vistas.
Paso 2. Asigna una variable.
Sea x el número de películas vistas.
Paso 3. Expresa la relación matemática.
Pago total = cuota fija (100) + 40 pesos por cada película:
CT = 100 + 40x
Paso 4. Escribe la ecuación lineal.
100 + 40x =
Paso 5. Resuelve la ecuación.
40x = 260 - 100
= 160
x = 160 / 40 = 4
→ Vio 4 películas.